纵观近几年公务员考试真题,无论是国考还是地方考试,集合问题作为一个热点问题几乎每年都会考到,此类题目的特点是总体难度不大,只要方法得当,一般都很容易求解。下面为大家介绍用数形结合方法解这类题的经典方法:文氏图。
一般来说,考试中常考的集合关系主要有下面两种:
1. 并集∪ 定义:取一个集合,设全集为I,A、B是I中的两个子集,由所有属于A或属于B的元素所组成的集合,叫做A,B的并集,表示:A∪B。
比如说,现在要挑选一批人去参加篮球比赛。条件A是,这些人年龄要在18岁以上,条件B是,这些人身高要在180CM以上, 那么符合条件的人就是取条件A和B的并集,就是两个条件都符合的人:18岁以上且身高在180CM以上。
2. 交集∩ 定义:(交就是取两个集合共同的元素)A和B的交集是含有所有既属于A又属于B的元素,而没有其他元素的集合。A和B的交集写作“A∩B”。形式上:x属于A∩B当且仅当x属于A且x属于B。
例如:集合{1,2,3}和{2,3,4} 的交集为{2,3}。数字9不属于素数集合{2,3,5,7,11} 和奇数集合{1,3,5,7,9,11}的交集。若两个集合 A 和 B 的交集为空,就是说他们没有公共元素,则他们不相交。
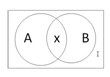
(I)取一个集合,设全集为I,A、B是I中的两个子集,X为A和B的相交部分,则集合间有如下关系:
A∩B=X,A+B=A∪B-X;文氏图如下图。
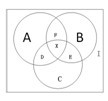
(II)取一个集合,设全集为I,A、B、C是I中的两个子集,D=A∩C,E=B∩C,F=A∩B,x为A、B、C的公共部分,即x=A∩B∩C,则集合间有如下关系:
A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C ;文氏图如下图
下面让我们回顾一下历年国考和地方真题,了解一下文氏图的一些应用。
例:如下图所示,X、Y、Z分别是面积为64、180、160的三个不同形状的纸片,它们部分重叠放在一起盖在桌面上,总共盖住的面积为290,且X与Y、Y与Z、Z与X重叠部分面积分别为24、70、36,问阴影部分的面积是多少?( )

A. 15 B. 16
C. 14 D. 18
——『2009年国家、中央公务员录用考试真题』
【答案:B】从题干及提供的图我们可以看出,所求的阴影部分的面积即(II)中的x,直接套用上述公式,我们可以得到:X∪Y∪Z=64+180+160,X∩Z=24,X∩Y=36,Y∩Z=70,则:
x=X∪Y∪Z-[X+Y+Z-X∩Z-X∩Y-Y∩Z]=290-[64+180+160-24-70-36]=16
从图上可以清楚的看到,所求的阴影部分是X,Y,Z这三个图形的公共部分。即图1中的x,由题意有:64+180+160-24-70-36+x=290,解得x=16。
例:旅行社对120人的调查显示,喜欢爬山的与不喜欢爬山的人数比为5:3,喜欢游泳的与不喜欢游泳的人数比为7:5,两种活动都喜欢的有43人,对这两种活动都不喜欢的人数是( )。
A. 18 B. 27 C. 28 D. 32
——『2009年广东省公务员录用考试真题』
【答案:A】欲求两种活动都喜欢的人数,我们可以先求出两种活动都不喜欢的人数。套用(I)中的公式:喜欢爬山的人数为120×58 =75,可令A=75;喜欢游泳的人数为120×712 =70,可令B=70;两种活动都喜欢的有43人,即A∩B=43,故两项活动至少喜欢一个的人数为75+70-43=102人,即A∪B=105,则两种活动都不喜欢的人数为120-102=18(人)。
例:某外语班的30名学生中,有8人学习英语,12人学习日语,3人既学英语也学日语,问有多少人既不学英语又没学日语?( )
A. 12 B. 13 C. 14 D. 15
——『2007年河南省公务员录用考试真题』
【答案:B】题中要求的是既不学英语又不学日语的人数,我们可以先求出既学英语又学日语的人数。总人数减去既学英语又学日语的人数即为所求的人数。套用上面的公式可知,即学英语也学日语的人数为8+12-3=17,则既不学英语又没学日语的人数是:30-(8+12-3)=13。
例:电视台向100人调查昨天收看电视情况,有62人看过2频道,34人看过8频道,11人两个频道都看过。问,两个频道都没有看过的有多少人?( )
A.4 B.15 C.17 D.28
——『2007年北京社招公务员录用考试真题』
【答案:B】本题解法同上,直接套用上述公式求出既看过2频道又看过8频道的人数为62+34-11=85人,则两个频道都没看过的有100-85=15人。





